Contoh Perhitungan Simple Beam

How to Analyze Support Reaction Simple Beam.
Berikut ini adalah contoh perhitungan Simple beam untuk beban terpusat dan untuk beban merata. Seblum masuk kecontoh perhitungan saya akan menjelaskan sedikit mengenai Hukum keseimbangan dan Reaksi Perletakan.

Perletakan (Tumpuan) adalah tempat kedudukan balok dan memperhatankan balok tetap pada kedudukan semula saat balok menerima beban.

Terdapat 3 jenis perletakan yaitu sendi, roll dan jepit.

1. Sendi, dapat menahan gaya vertikal dan gaya horizontal
2. Roll, dapat menahan hanya gaya vertikal.
3. Jepit. Mampu menahan gaya vertikal, Horizontal dan momen.

Agar Struktur dalam keadaan seimbang maka suatu reaksi harus memenuhi kriteria dibawah ini.

Aksi  = Reaksi

Aksi - Reaksi = 0

Hukum kesimbangan suatu reaksi adalah jika :

Sigma Gaya Vertikal = 0

Sigma Gaya Horizontal = 0

Sigma Momen = 0

Berikut ini adalah contoh perhitungan penyelesaian dari simple beam.

Beban Terpusat

Pertama Kita akan mencara reaksi perletakan pada tumpuan A dan Tumpuan B

∑ Mb = 0   ,                                                                         ∑ Ma = 0
    Ra . 8 - P1.4 = 0                                                               Rb . 8 - P1 . 4 = 0
    8 Ra  - 8 . 4  = 0                                                               8 Rb  -  8  .  4  = 0
    8 Ra  = - 32                                                                      8 Rb  =  - 32
    Ra  =  - 32 /8                                                                    Rb  =  - 32 /8
    Ra  =  4 KN                                                                      Rb = 4 KN

Selanjutnya Kita Kontrol Sigma V = 0

Ra - P1 + Rb = 0
4  -  8  -  4 = 0 (Ok Komponen Seimbang)

Selanjutnya Menghitunga Momen dan gaya geser :

Momen
untuk menghitun momen simple beam diatas dibagi menjadi 2 tinjauan. Untuk tinjauan 1 dari jarak 0 sampai 4 meter. Sedangkan untuk tinjauan dua dari 4 meter samapi dengan 8 meter.

Tinjauan 1 ( 0 Meter - 4 Meter )
∑Momen  = 0

Mx  =  Ra . x  =  0  ( Subtitusi Nilai X/Jarak dan Nilai Ra )

Untuk Nilai X = 0 ; 4 . 0 = 0 KNm
Untuk Nilai X = 1 ; 4 . 1 = 4 KNm
Untuk Nilai X = 2 ; 4 . 2 = 8 KNm
Untuk Nilai X = 3 ; 4 . 3 = 12 KNm
Untuk Nilai X = 4 ; 4 . 4 = 16 KNm

Tinjauan II ( 4 Meter - 8 Meter)
Momen = 0
Mx = Ra . x -  P. (x-4) = 0 (Subtitusi Nilai X/Jarak dan Nilai Ra). Catatan : Untuk X = 4 Harus sama nilainya dengan tinjauan 1 dikarenkan tinjauan II merupakan kelanjutan dari tinjauan I.

Untuk Nilai X = 4 ; 4 . 4 - 8 . ( 4 - 4 ) = 16 KNm
Untuk Nilai X = 5 ; 4 . 5 - 8 . ( 5 - 4 ) = 12 KNm
Untuk Nilai X = 6 ; 4 . 6 - 8 . ( 6 - 4 ) = 8 KNm
Untuk Nilai X = 7 ; 4 . 7 - 8 . ( 7 - 4 ) = 4 KNm
Untuk Nilai X = 8 ; 4 . 8 - 8 . ( 8 - 4 ) = 0 KNm

Bisa dilihat berdasarkan perhitungan momen pada tiap ujung = 0 dikarenkan tidak ada momen yang bekerja pada ujung tumpuan dikarenakan mengunkan sendi dan roll.

GAYA GESER (Q)
Sama dengan menghitung besarnya momen, untuk menghitung gaya geser pada simpel beam tersebut ditinjau dari 2 tinjauan.

Tinjauan 1 (0 Meter - 4 Meter)
Qx  =  Ra
Q1 - Q4 = Ra  = 4 KN

Tinjauan II ( 4 Meter - 8 Meter )
Qx  = Ra - P1
Q4 - Q8  = 4 - 8 = -4 KN

Dan pada ujung dinjauan 2 = Ra - P1 + Rb = 4 - 8 + 4 = 0.

Kira kira jiga digambarkan kedalam diagram seperti dabawah ini.

BEBAN TERBAGI MERATA

Langkah Pertama sama seperti diatas yaitu mencari reaksi pada perletakan atau tumpuan.

W =  q . L  = 4  .  8  = 32 KN


∑Mb = 0                                                                               ∑Ma = 0
Ra . 8  - W . 4 = 0                                                                    Rb . 8 - W . 4 = 0
8Ra  -  32 . 4 = 0                                                                      8 Rb  -  32  . 4 = 0
8Ra =  128                                                                               8 Rb  =  128
Ra  =  16 KN                                                                            Rb = 16 KN

Kontrol Sigma V = 0 ; 16 - 32 + 16 = 0

GAYA GAYA DALAM

MOMEN
Tinjauan I
Mx  =  Ra . x -  q x . 1/2X     ; ~ 1/2 x jarak setengah bentang
Mx  =  16x - 2x^2 ----------- > Untuk Letak Momen Maximum 16 - 4x = 0 ~ x=4 Meter

M0 = 16.0 - 2.0^2 = 0
M1 = 16.1 - 2.1^2 = 14
M2 = 16.2 - 2.2^2 = 24
M3 = 16.3 - 2.3^2 = 30
M4 = 16.4 - 2.4^2 = 32 (Momen Maxiumum)
M5 = 30
M6 = 24
M7 = 14
M8 = 0

GAYA GESER
Tinjauan I
Qx  =  Ra  -  q . x
Q0  =  16  - 4 . 0 = 16
Q1  =  16  - 4 . 1 = 12
Q2  =  16  - 4 . 2 = 8
Q3  =  16  - 4 . 3 = 4
Q4  =  16  - 4 . 4 = 0
Q5  =  16  - 4 . 5 =  -4
Q6  =  16  - 4 . 6 =  -8
Q7  =  16  - 4 . 7 =  -12
Q8  =  16  - 4 . 8 =  -16

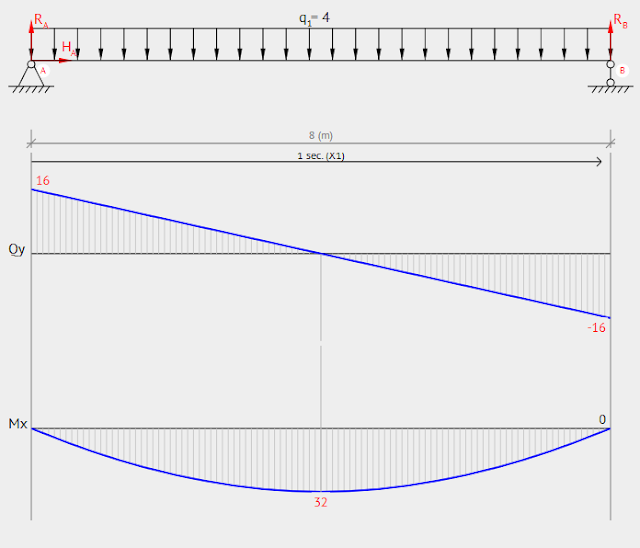
Berikut gambar grafiknya :

Demikianlah Artikel Diatas semoga bermanfaat.

Baca Juga